Bubble Sort C++

Bubble sort is a sorting algorithm that compares two adjacent elements and swaps them until they are in the intended order.

Just like the movement of air bubbles in the water that rise up to the surface, each element of the array move to the end in each iteration. Therefore, it is called a bubble sort.

Working of Bubble Sort

Suppose we are trying to sort the elements in ascending order.

1. First Iteration (Compare and Swap)

1. Starting from the first index, compare the first and the second elements.
2. If the first element is greater than the second element, they are swapped.
3. Now, compare the second and the third elements. Swap them if they are not in order.
4. The above process goes on until the last element.

   

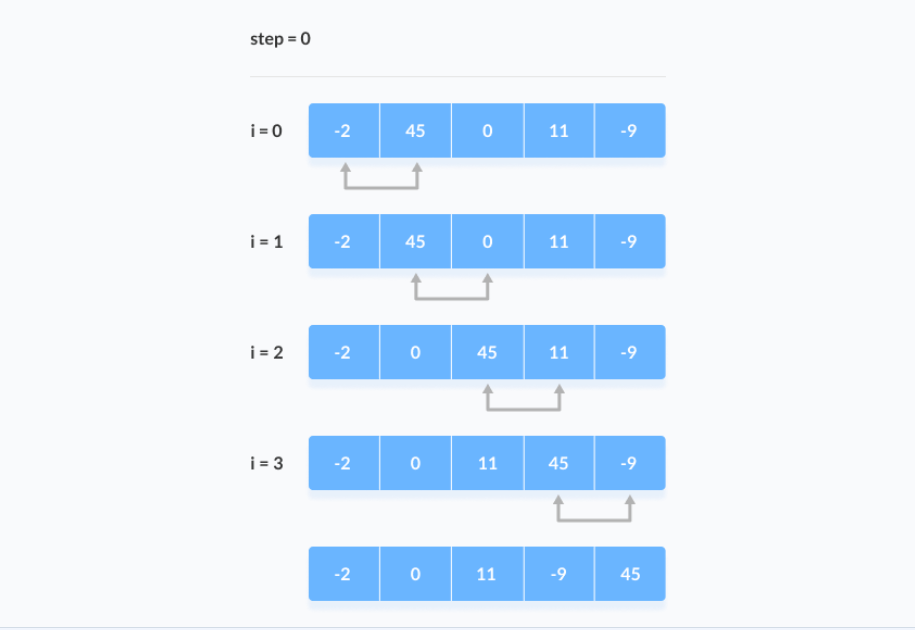   Compare the Adjacent Elements

2. Remaining Iteration

The same process goes on for the remaining iterations.

After each iteration, the largest element among the unsorted elements is placed at the end.

Put the largest element at the end

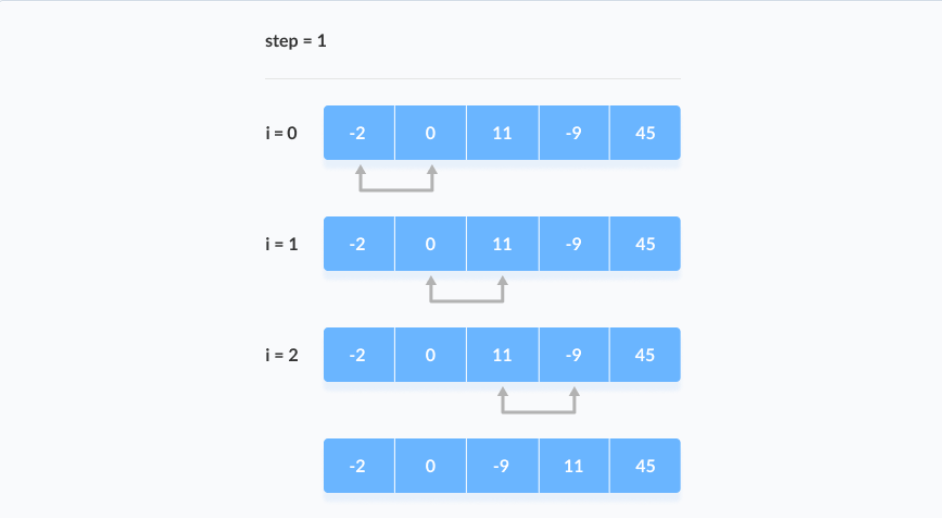
In each iteration, the comparison takes place up to the last unsorted element.

Compare the adjacent elements

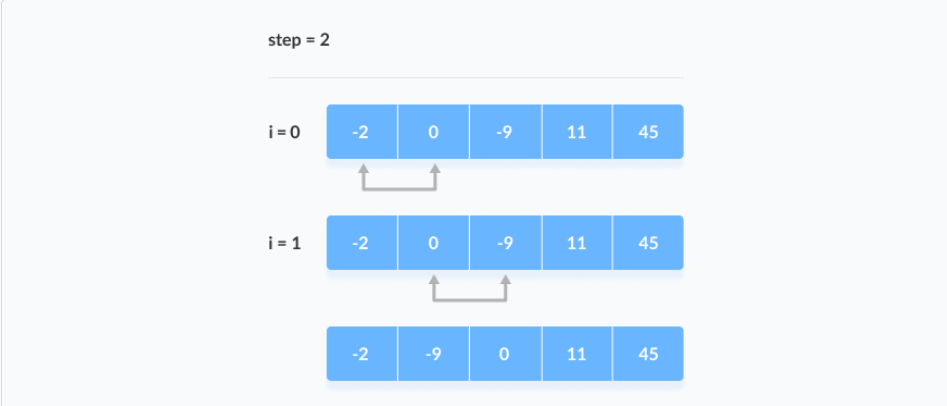
The array is sorted when all the unsorted elements are placed at their correct positions.

The array is sorted if all elements are kept in the right order

Bubble Sort Algorithm

                  
        bubbleSort(array)
          for i <- 1 to indexOfLastUnsortedElement-1
            if leftElement > rightElement 
              swap leftElement and rightElement
        end bubbleSort
      
    

Bubble Sort Code in C++

      // Bubble sort in C++
      
      #include <iostream>
      using namespace std;
      
      // perform bubble sort
      void bubbleSort(int array[],int size) {
      
        // loop to access each array element
        for (int step = 0; step < size; ++step) {
            
          // loop to compare array elements
          for (int i = 0; i < size - step; ++i) {
      
            // compare two adjacent elements
            // change > to < to sort in descending order
            if (array[i] > array[i + 1]) {
      
              // swapping elements if elements
              // are not in the intended order
              int temp = array[i];
              array[i] = array[i + 1];
              array[i + 1] = temp;
            }
          }
        }
      }
      
      // print array
      void printArray(int array[], int size) {
        for (int i = 0; i < size; ++i) {
          cout << "  " << array[i];
        }
        cout << "\n";
      }
      
      int main() {
        int data[] = {-2, 45, 0, 11, -9};
        
        // find array's length
        int size = sizeof(data) / sizeof(data[0]);
        
        bubbleSort(data, size);
        
        cout << "Sorted Array in Ascending Order:\n";  
        printArray(data, size);
      }

Optimized Bubble Sort Algorithm

In the above algorithm, all the comparisons are made even if the array is already sorted.

This increases the execution time.

To solve this, we can introduce an extra variable swapped. The value of swapped is set true if there occurs swapping of elements. Otherwise, it is set false.

After an iteration, if there is no swapping, the value of swapped will be false. This means elements are already sorted and there is no need to perform further iterations.

This will reduce the execution time and helps to optimize the bubble sort.

Algorithm for optimized bubble sort is

      bubbleSort(array)
        swapped <- false
        for i <- 1 to indexOfLastUnsortedElement-1
          if leftElement > rightElement
            swap leftElement and rightElement
            swapped <- true
      end bubbleSort

Optimized Bubble Sort in C++

            

  
      // Optimized bubble sort in C++
      
      #include <iostream>
      using namespace std;
      
      // perform bubble sort
      void bubbleSort(int array[],int size) {
          
        // loop to access each array element
        for (int step = 0; step < (size-1); ++step) {
            
          // check if swapping occurs
          int swapped = 0;
          
          // loop to compare two elements
          for (int i = 0; i < (size-step-1); ++i) {
              
            // compare two array elements
            // change > to < to sort in descending order
            if (array[i] > array[i + 1]) {
      
              // swapping occurs if elements
              // are not in intended order
              int temp = array[i];
              array[i] = array[i + 1];
              array[i + 1] = temp;
              
              swapped = 1;
            }
          }
      
          // no swapping means the array is already sorted
          // so no need of further comparison
          if (swapped == 0)
            break;
        }
      }
      
      // print an array
      void printArray(int array[], int size) {
        for (int i = 0; i < size; ++i) {
          cout << "  " << array[i];
        }
        cout << "\n";
      }
      
      int main() {
        int data[] = {-2, 45, 0, 11, -9};
        
        // find the array's length
        int size = sizeof(data) / sizeof(data[0]);
        
        bubbleSort(data, size);
        
        cout << "Sorted Array in Ascending Order:\n";
        printArray(data, size);
      }